The power of multiple approaches

Graphs are a wonderful tool for students to solve maths problems. They allow them to
visualise answers, which can be less obvious when using an algebraic approach. The
advantage of using a graphic calculator is evident in this scenario. It offers numerous ways
to approach mathematical problems, which makes students feel more confident as they can
cross-check their work or use the most appropriate method for a particular scenario. Another
benefit is that graphic calculators encourage students to exhibit their work and explain their
thought processes. We spoke with Mathematician Simon May, who demonstrated different
techniques to solve the same mathematical problem using the fx-CG50 handset.
Since there are countless ways to solve the same problem using the handset, we’ll focus on
some interesting approaches to solving trigonometry questions using the fx-CG50 and its
graphing features.

Angles are angels

Gone are the days of students being afraid of questions with angles, especially in
trigonometry. Using the features of fx-CG50, students can be more confident than ever
about the answers they get.

In a straightforward trigonometry question, students can expect to enter the expression on
the screen and press EXE and get the result. But when things get more complex, a more
sophisticated tool like the graphing system should be used.

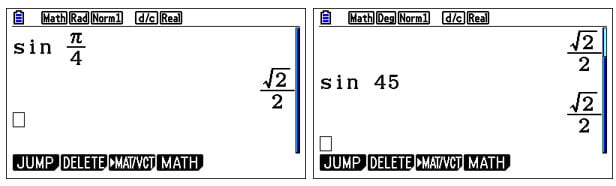
Remember that selecting the proper units when doing calculations is very important, especially in trigonometry. For example, the default unit for angles is radians, but in questions where real-life applications are tested e.g. elevations, it’s wise to switch to degrees, says our Maths Expert, Simon.

In Maths, like in life, there can be multiple solutions to a problem. For example, when we find the value of x using the SolveN function where `Sin x=0.3`, we expect multiple solutions. The handset neatly gives the answers as a restricted “set”. But traversing items in a set horizontally can be unintuitive. The solution to this problem is to press `EXE`, and there you go! The answers are now displayed as a much more user-friendly “List”.

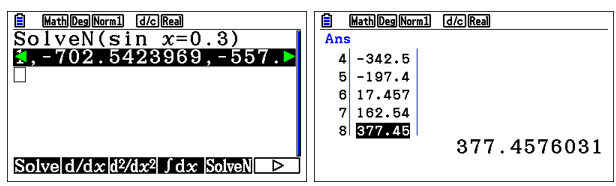
Sometimes, depending on the context, students only need to display values within a certain range. One trick Simon has for students is to remove answers that are not relevant. For example, he mentions that angles of elevation greater than90 degrees effectively mean looking backwards. Also, bearings greater than 360 degrees suggest a complete rotation and beyond, which is also not useful in most cases, he adds. Therefore, by eliminating, students can narrow their focus to a handful of options.

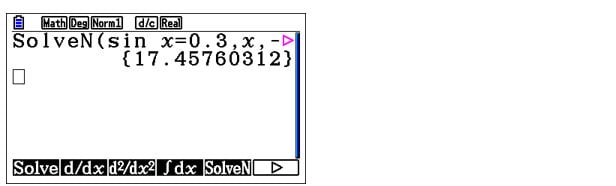
While students can think about all of this and reject the superfluous answers by themselves, it would be great only to display the values which are really of use, wouldn’t it? Students can do just that by entering a few more arguments in the `SolveN` function as shown.

`SolveN` is much better than the `Solve` function because the former gives multiple solutions when available in a very straightforward manner while the latter doesn’t. To quote Simon, “`Solve` is like the grandfather of the new, shiny and more powerful `SolveN`.”

Graph on it!

Suppose your students, who are often particularly careful, wish to examine their expressions using the graph mode. One caveat is that selecting the proper unit of angles is very important. Otherwise, the graph wouldn’t make sense. If needed, students can even use the `TRIG` setting, which sets the ranges of the axes of the graph to proper values to see the variations of the graph clearly. To access it, press ‘V-Window.

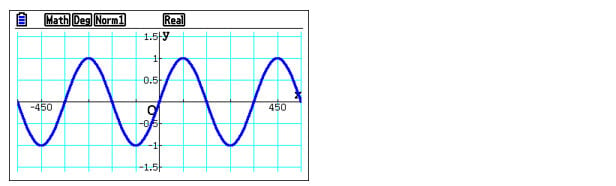
To find the values of the intersection points, students can use the `G-SOLVE` feature’s `INTSECT` option. When enabled, this gives the students a chance to see a cursor that can be moved between the intersection points using the keypad arrows.

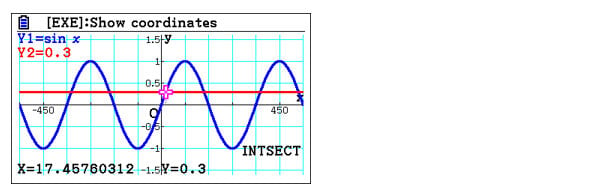
Visualising a graph gives students an added advantage, allowing them to see various details that would be impossible to see with just expressions and written functions. For example, it’s clear that there is a line of symmetry at 90 degrees.

So if the intersection point to the left is at x≈17, students can guess that the intersection point on right is at x≈180-17. Another interesting mention by Simon is the displayed x values can be extracted through variables into the calculation matrix. This is effectively what we did in a previous blog where we used the clip function to copy Maths functions, but here we copy calculated results instead.

Those were some ways where students could use various features of the handset to deal with calculations and their results.

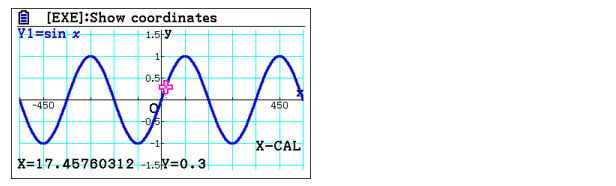
Another awesome feature for students to try out is to input an arbitrary  y value in graph mode to see the corresponding  x value. The movable cursor is then placed at this coordinate. Also, since the calculator is smart enough to have all the intersection points calculated by itself in the background (even when only one graph is drawn), students can still jump between the intersection points using the keypad arrows. The value of x calculated this way is called “X-CAL”.

In graph mode, you can even have a new function which is equal to the difference between two other functions. For example, to draw , enter Y3=Y1-Y2. Here, students don’t have to copy and paste the functions using in-built functions such as clip.

When there are multiple functions drawn in the graph mode, students can always select which function to analyse using the keypad arrows.

Equation mode

In the Equation mode, there is a powerful feature “Solver”, which according to Simon, “Not many students use efficiently.” This is somewhat similar to the “Solve” function in Run matrix because it gives only one answer value at a time. The real power of “Solver” can be demonstrated by taking an example.

If students want to find the value of they can keep entering values for X until they get a realistic answer.

We can take another example where we use SolveN to solve the equation . We can approach the same problem graphically by drawing the two trigonometric functions on the above equation’s left and right sides. A student can solve this problem either using intersect method or the root method (subtracting one function from the other). An algebraic method for the specific example can be explored by drawing a third function with the equation.

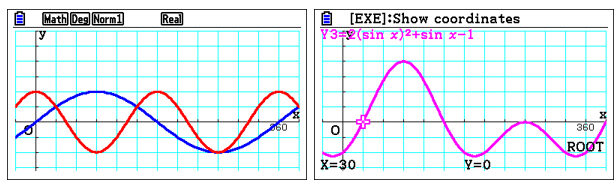
As Simon puts it, “Since the value of the magenta curve should be zero wherever the blue and red curves intersect, it’s a way of confirming that you got the correct algebraic form for the magenta curve.”

In trigonometry, one of the hardest things is to remember the equations which are equivalent to some others. Using the graph method to check whether these curves fit how they are supposed to, a student can easily confirm whether their memory is correct, which would save time and valuable marks during an exam.

Integration tricks

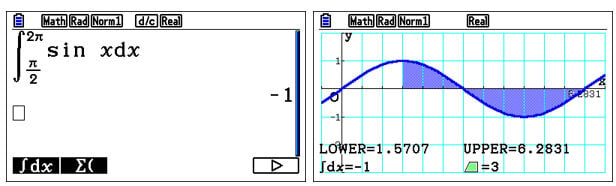
Suppose a student is given a question which may need them to evaluate an integral, integrating numerically would provide a quick value, however, it would be very wise to use the graph mode to draw the function first The solution can be found by using the integral option in the G-SOLVE menu. Here the students can enter the lower and upper bounds, and the handset will shade the area and give the answer in a moment.

Simon stresses the importance of the sign of the answer in such questions since some part of the area is above, and some part is below the X-axis, which may be contextually important. Therefore, the MIXED integration option can be used to view the actual area (both above and below) covered by the graph in the range.

Hands-on experience

Understanding the available approaches that can be used to solve various Mathematical problems is a nice thing to have in a student’s toolbox. They can use this knowledge to select the best approach to solve problems based on the context. This saves them valuable marks and time, which is a huge plus during an exam. It’s important to understand that these approaches have their own advantages and limitations, which the students should use and get hands-on experience with.

Book a training!

We brought you these interesting tips and tricks on multiple approaches to solving a Maths problem using the fx-CG50 handset. As Simon puts it, “There’s not just one way of doing things, but multiple ways with pros and cons. It’s up to the students to select which one to use during an exam by making an informed decision.”

If you want to help your students achieve even more, why not signup for our free skills training sessions? One good reason you should signup for the training is that these sessions are run by experts on the calculator, and therefore it will be a great opportunity to learn from them and, yes, for free!