Supporting Students as They Transition from GCSE to A Level Maths

At the start of A Level Maths, there’s a fair bit of overlap between topics first covered in GCSE.

It’s an important transition time, ensuring all students transitioning to A Level have the fundamentals in place. Often this time includes covering topics first visited at GCSE, with a focus on building strong foundations for students as they progress through their A Level.

Importantly, for most students, A Level will be the first time they use a graphic calculator. Many students at GCSE won’t have a graphing calculator before, so having a graphing calculator is quite exciting and opens up all sorts of probabilities.

There are a few apps in the main menu on the fx-CG50 that are good for just going over GCSE topics and what students need to know. The obvious one is Run Matrix, which is where students go to do all the basic calculations. But, also, Equation mode is quite useful. You also have Graph mode, which will be new to most students and is important to get them familiar with solving problems graphically. You could also use Conic graphs a little because that has quadratics in there, which they need to know about and would’ve seen before.

We spoke with mathematician Simon May to explore how these apps in the fx-CG50 can support teaching during this important transition period.

 

Familiarising students with Run Matrix

Students will learn about square roots and surds at GCSE and a certain amount of index laws. At the start of A Level, the focus is on refreshing this understanding and getting students familiar with how their calculator can help them investigate and validate.

For example, exploring two raised to the power of 1/3 and investigating what happens when they multiply that by two raised to the power of 1/3? They’ll have the cube root of two times the cube root of two. Now students could be confused by this and say it’s going to give two, and they’re squaring it. But the square of the cube root gives you a horrible decimal because it’s two raised to the power of 2/3.

Using the calculator, you can reinforce the index rules when teaching this by saying, what is two raised to the power of 2/3? Students will see they have the same value.

Students can also go back to previous calculations to explore in more detail. For example, they could edit what they’ve inputted, and instead of having two to the power 1/3, they could turn that into two to the power of a 1/4. You have two to power quarter times two to power third. What is that going to be? It gives me this horrible decimal. But then they could investigate further and use the calculator to confirm their suspicions.

In Run Matrix, they can do a calculation in one line and then confirm it with their answer underneath. Seeing the same answers affirms that there is a rule and helps reinforce their understanding.

 

Exploring Equation

The next thing to look at with students is Equation. Here students can solve simultaneous, polynomials and general equations. Before A Level, they would probably be aware of simple quadratic equations, and you can start them off with solving a quadratic here, for example, asking what happens if you have 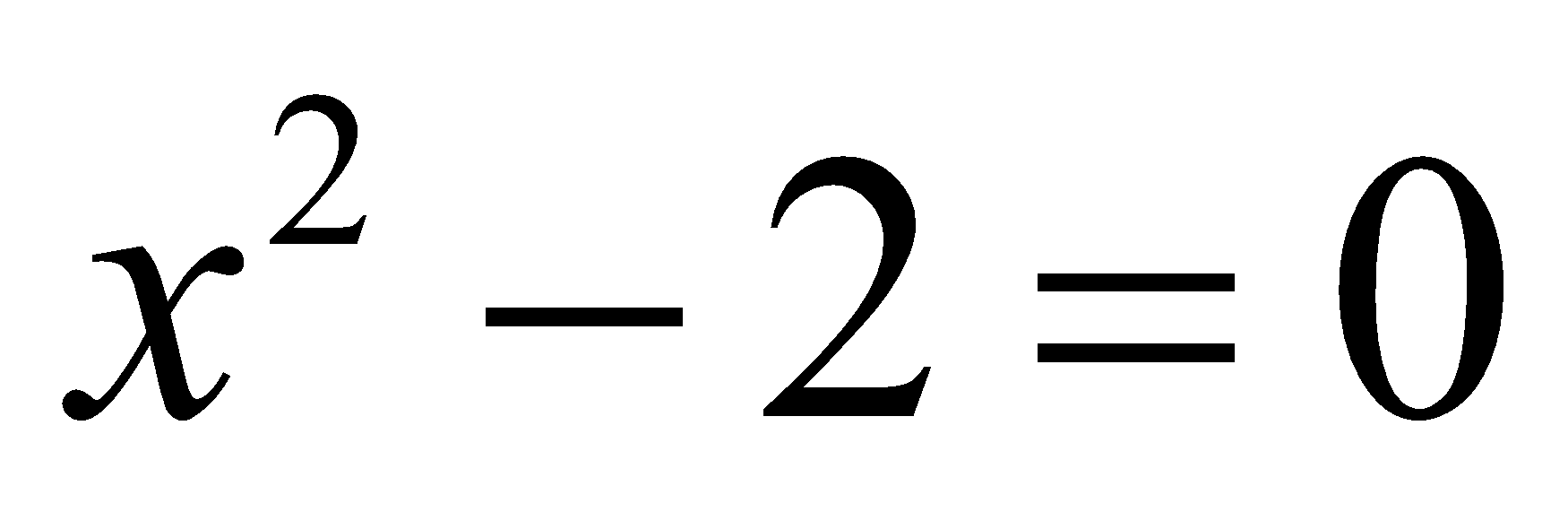. Students will get the answer is the square root of two. The nice thing here is that it answers a decimal in the list. However, if the calculator can, it provides a surd. Then they can extend that to a slightly more complicated quadratic to extend their understanding.

Spending time exploring this functionality gives them a chance to improve how they will attempt to solve these equations, as they can use more than one method.

You can also confirm the answer by going back to Run Matrix, using the SolveN menu that they will not have seen before, to solve something like 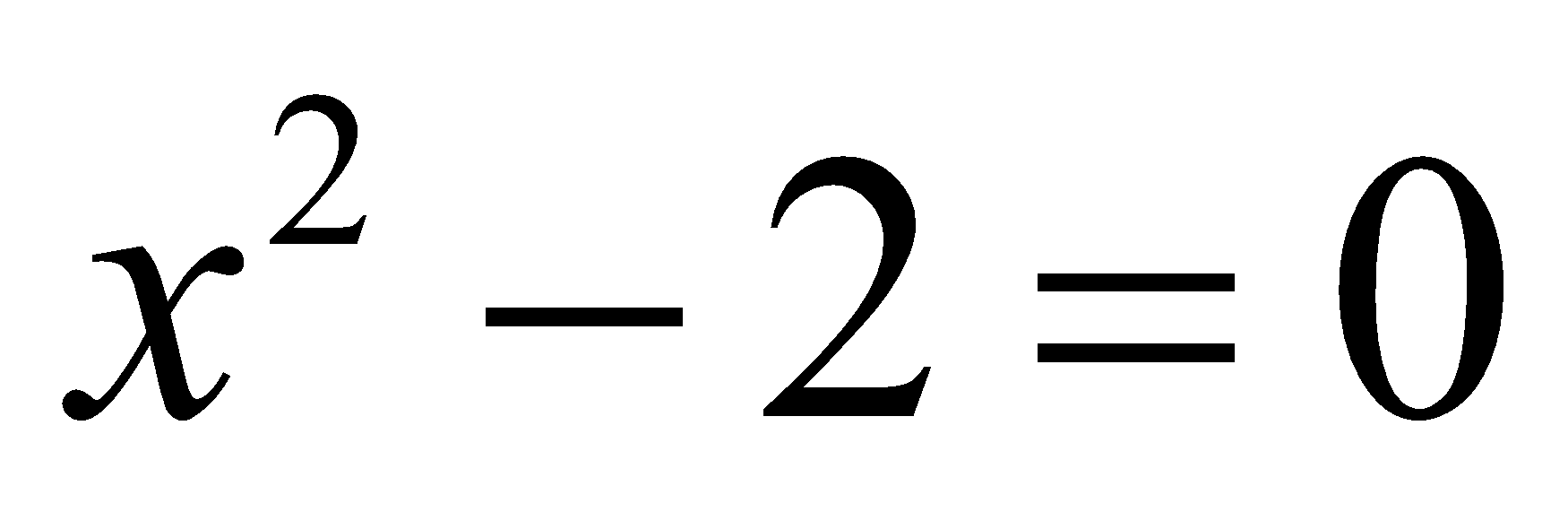 Often, it blows students away because the calculator gives them the surds and all the answers simultaneously. It’s a useful feature for students to learn or use at the beginning of that A-Level career, so they’re familiar with it as they explore more complicated equations.

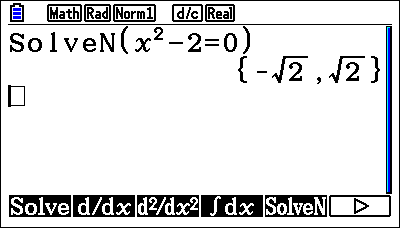
Going back to Equation, you also have Solver where students can input complete equations and solve for changing variables. Students will likely already know the Simultaneous Equation feature, as it’s available on ClassWiz handsets, and here they approach simultaneous equations as they did before. But it’s worth showing them where it is on the graphic calculator, so they know it’s still available to us.

Approaching problems graphically

Graph mode is, understandably, one of the big changes when starting A Level maths, and it’s often the first introduction students will have to solve problems graphically on their device. Teachers probably use graphs when teaching it at GCSE, but the students can’t get hands-on with the graphs to solve it because they won’t have the handset.

A nice place to start at A Level is with simultaneous equations. These get more complicated because they can mix linear and quadratic equations, so straight lines and curves.

With Graph mode, you can sketch two functions and draw them. Solving these graphically gives a better understanding of what’s happening, as students have the visual prompt to aid them. For example, if you ask students to solve 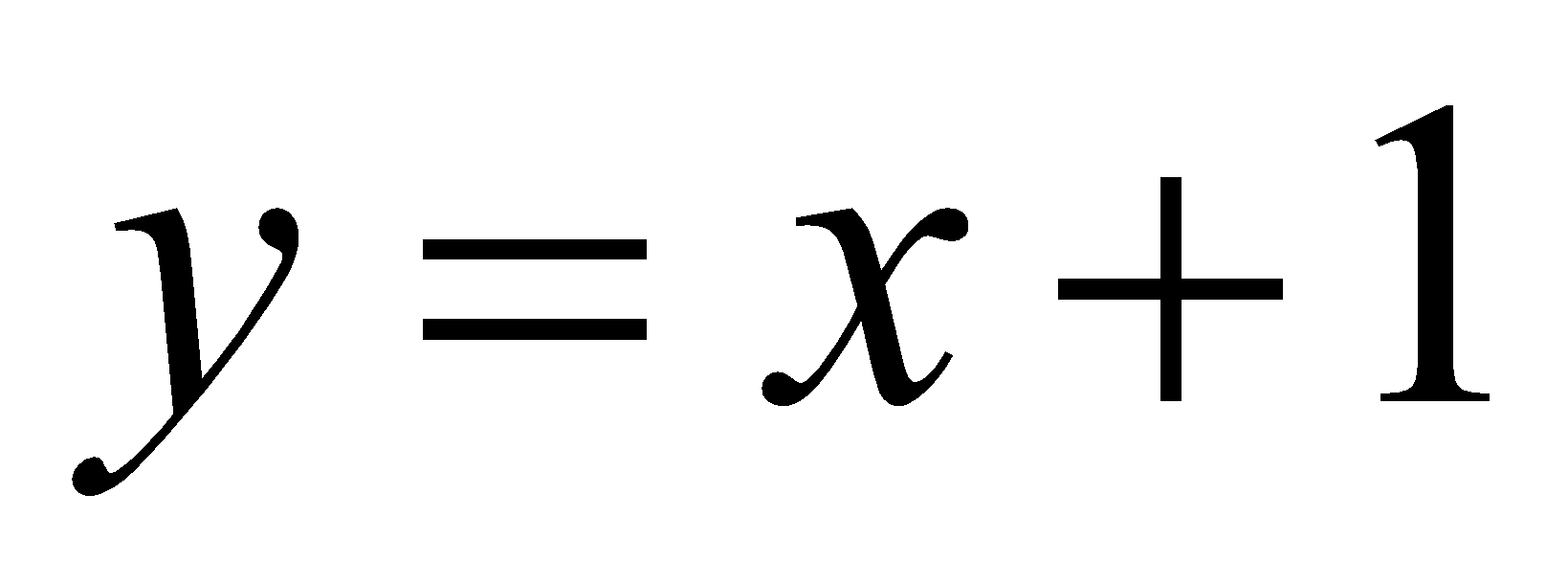 and 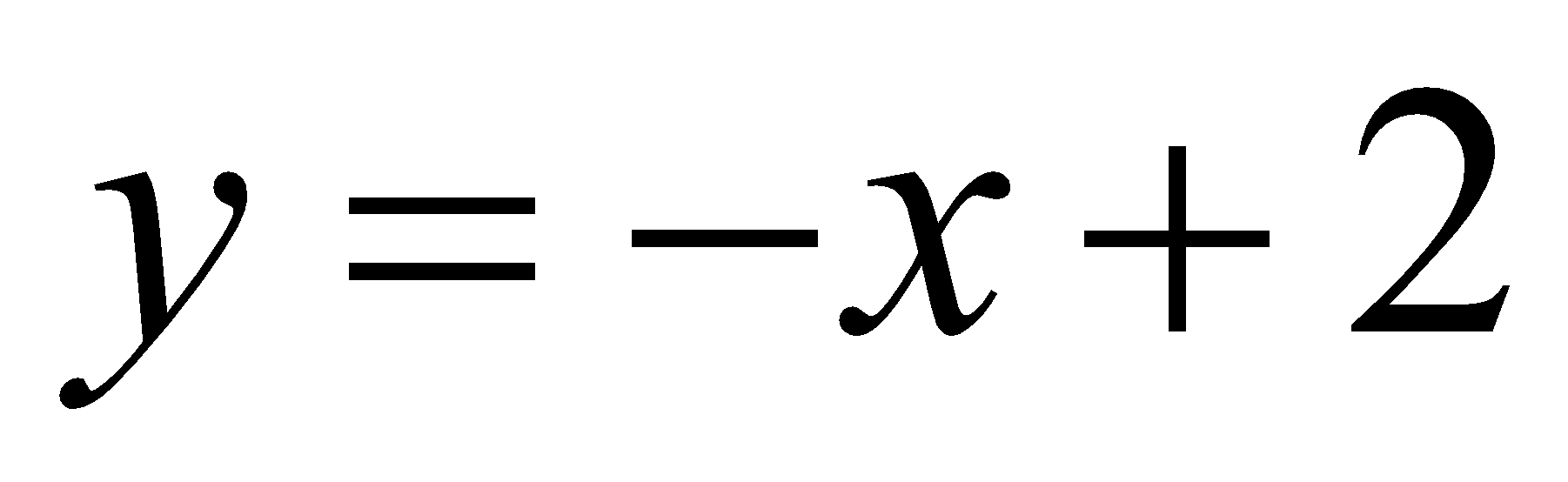 simultaneously, some students will get thrown by this request. But it becomes much clearer if they draw the two lines and can see where they cross.

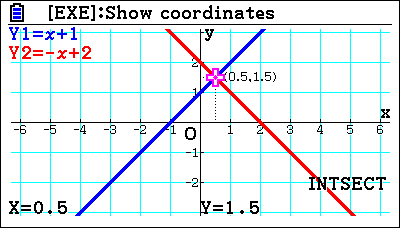
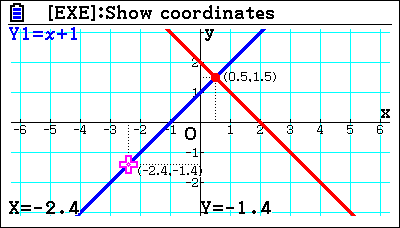
Students can also trace a point, moving it along to see the values, which is a very fast way of seeing what the values are in a function. It’s possible to use Table mode for this, but that will only give the values for the one function and the different table values.

When you are talking about a quadratic, students need to be able to sketch them, and they’ve got to be able to put them in the right place. Normally you start with something simple like X squared and then build from this point. For example, asking students, “What happens if you move it?”. Students won’t have used modify before; modifying allows them to change what’s happening. And that’s quite a powerful tool because if you say, in this case, if B is two, how did it change from the previous Graph?

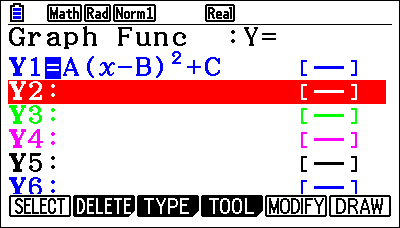
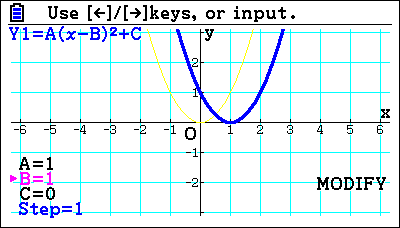
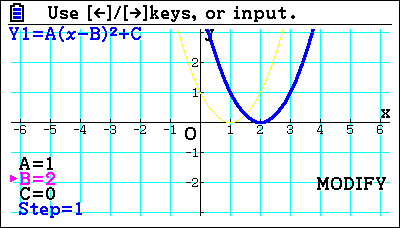
Students can do the intersections, which is the same as using graphs to solve simultaneous equations. Once they’ve solved two lines where they cross, they can move on to solving lines and curves. It’s a nice developmental step, from equating two functions. For example,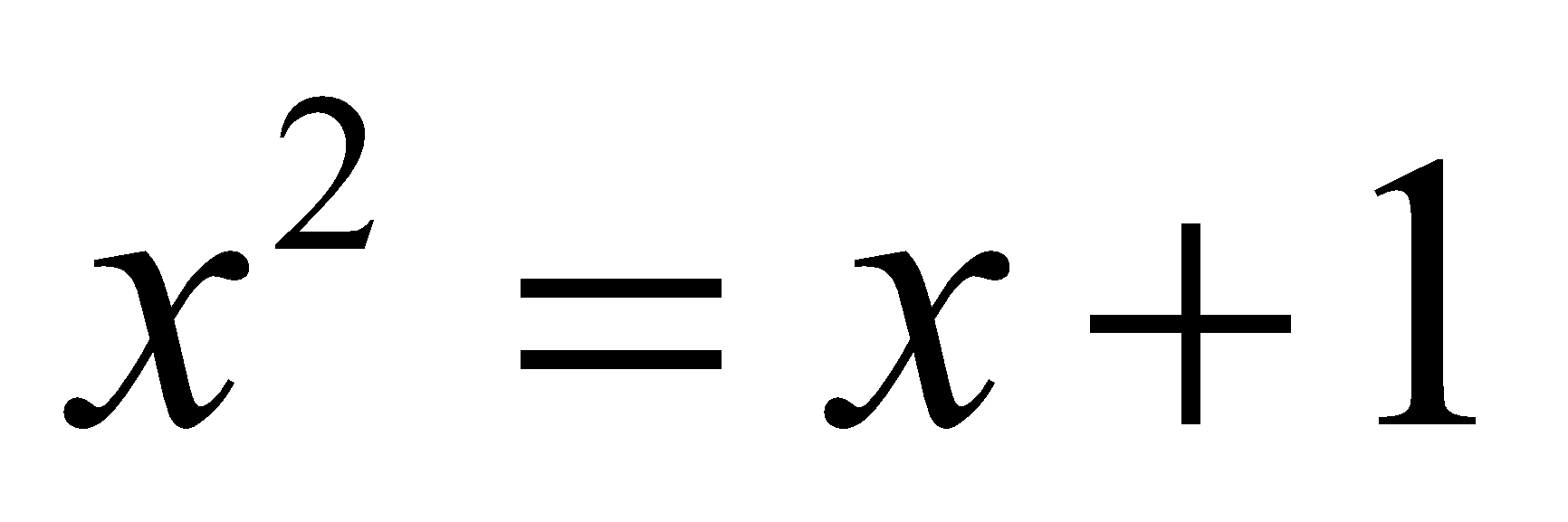 

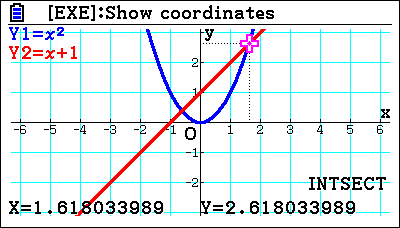
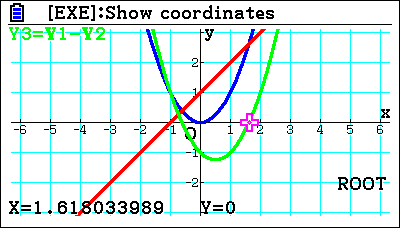
But they can also then set that equal to zero. For example, they can do Y1-Y2. They can draw that, and where it equals zero, they can see where they are crossing. It’s a useful teaching point because that’s what they would do when trying to solve it algebraically; they would equate the two equations, turn them into a quadratic and solve it.

If students study quadratics, one of the first ways they’d probably learn how to solve them is to factorise them. In Graph, it is quite neat because they can turn it into two factors, so that, for example, 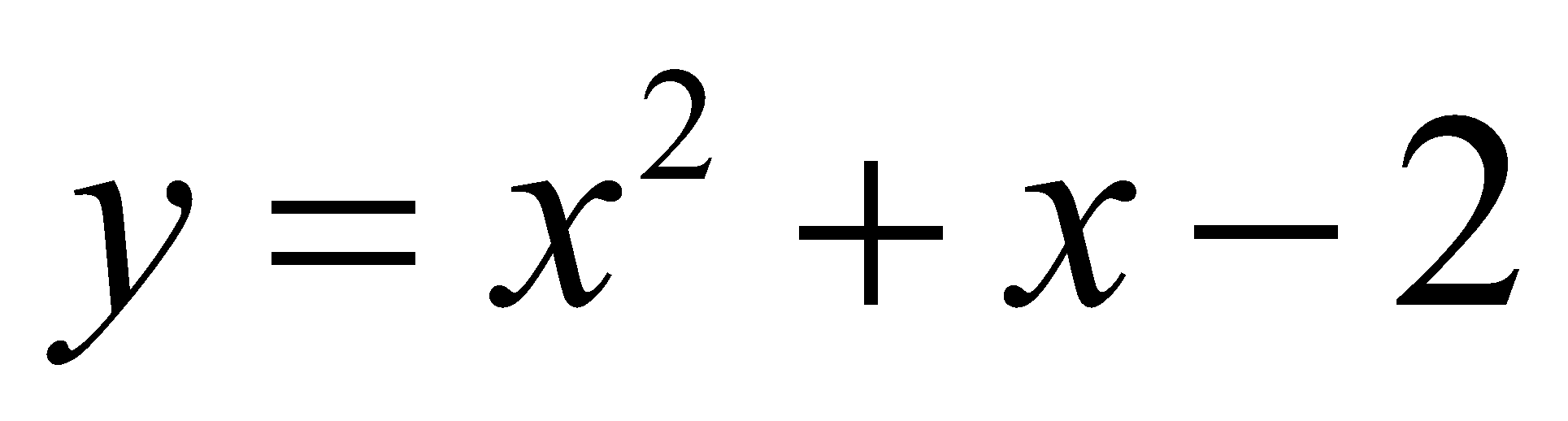  factorises to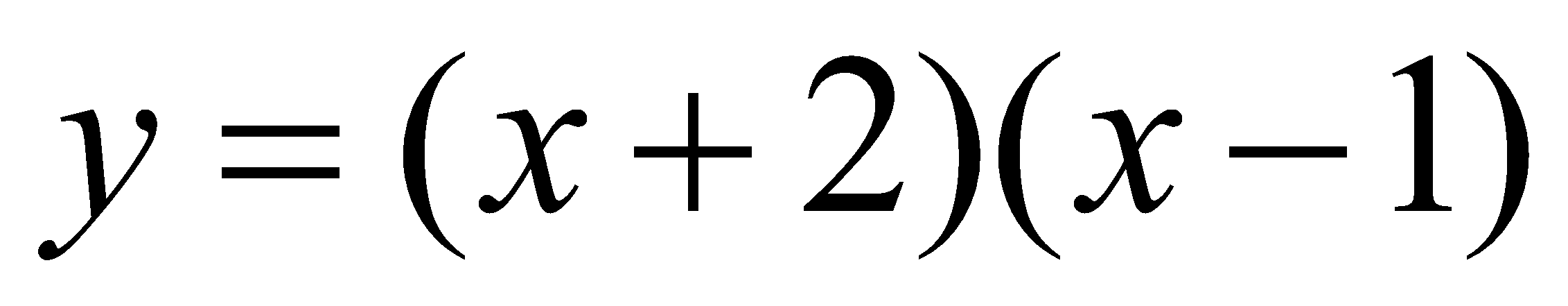 

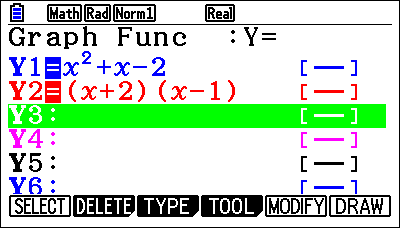
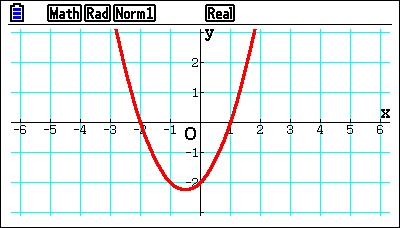
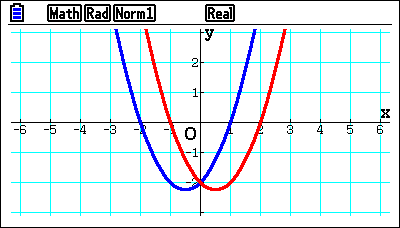
Then, if students have a quadratic and are unsure whether you’ve factorised it correctly, they can just put their quadratic in and see if the graphs are coincident. Whether expanding brackets, turning them into the quadratic or factorised quadratic to turn them into brackets, it works both ways. This feature helps students get on top of that because if they get the factorisation the wrong way or stick some different values in there, they’d get a different graph. It helps them recognise that they’ve gone wrong, improving their confidence.

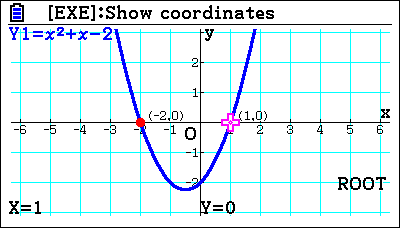
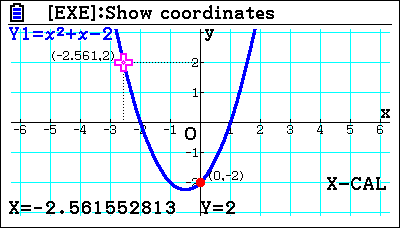
You also have the y-intersection or even the roots. So if you have sketched it and you find the roots negative two and negative one, that directly links into the factors.

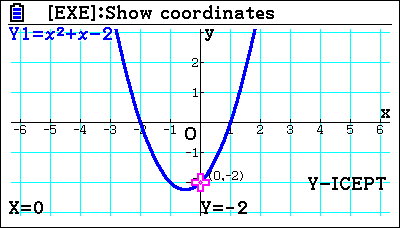
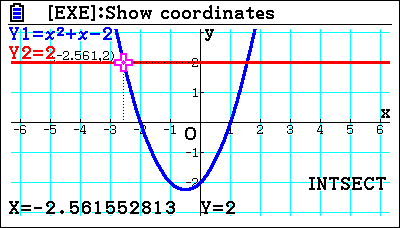
You can trace a point if you want, but you can investigate the minimum point of it automatically finds those. It finds the Y intercept, which in this case is Y equal negative two and that is directly linked to that value? You can also calculate some plain old values. What’s the Y value when X is this, or even better, what is the X value when Y is this? So you’re working backwards? You can say, when Y equals two, what’s the value of X? The other way of approaching that would be to say, ” Let’s enter the line Y equals two. And then you can find the intersections, which is a nice teaching tool. When Y equals two and the quadratic intersects, it makes no difference that the line is horizontal. It’s just another line, but students do struggle with the idea of saying well, “What happens when this quadratic equals two or visually?”. If they can draw it, it becomes clearer to them what is happening.

Conclusion

Run Matrix, Equation and Graph are the big ones at the start of the year, and will be important for students throughout their A Level. The features in these apps provide a lot of useful teaching points that can reinforce learning.

Want to know more about the key features available on the fx-CG50 graphic calculator? We provide free skills training sessions, which are run by experts familiar with using the calculator to support learning in the classroom.