How modelling calculator use boosts student learning

Your approach to using calculators in lessons can have a powerful influence on how students approach maths. Real-time modelling gives an insight into your problem-solving process, highlights multiple strategies for tackling questions and illustrates how mistakes can lead to important learning moments.

In this blog, we dive into how you can use calculators in your teaching, with classroom examples illustrating how demonstrations can spark curiosity and support better problem solving.

Modelling problem solving in real time

Using a calculator to help you work through a problem in front of a class allows you to make your thinking visible. Students see that maths isn’t just about finding an answer – it’s also about experimenting with different approaches, making connections and adapting their strategy if needed.

Demonstrating multiple methods on the calculator is particularly useful for reinforcing the idea that problems can be solved in different ways. As well as helping students learn flexibility and gain confidence in their own strategies, this can feed into deeper conceptual understanding of the topic in question.

Let’s take the example of quadratic equations – a topic you might be introducing to a GCSE class or reinforcing with some year 12s who have just started A-level maths.

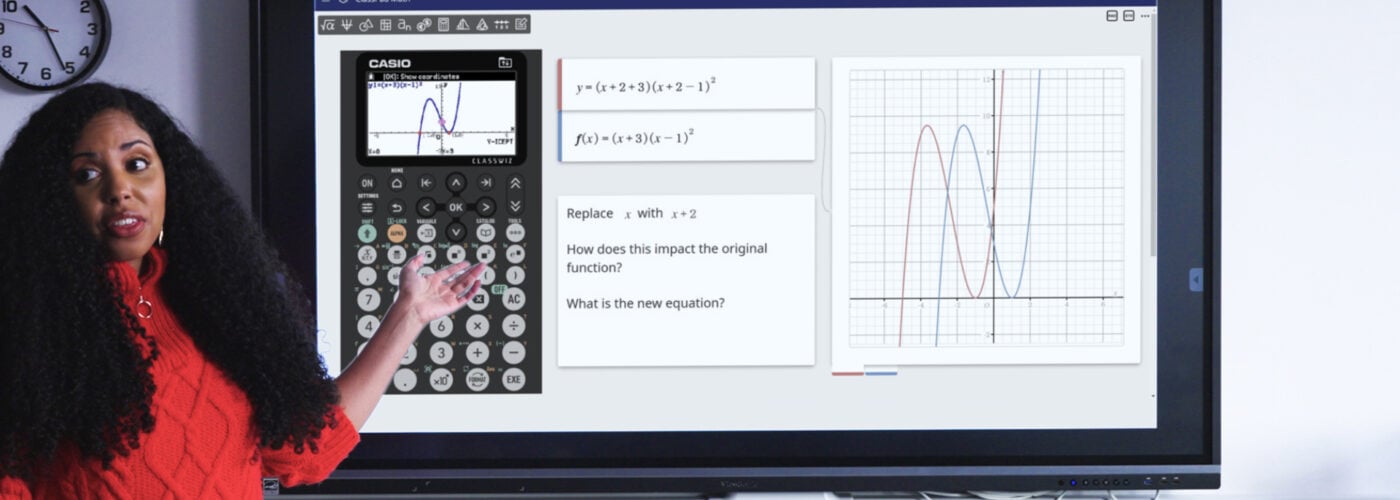
On the fx-CG100 graphic calculator, you can solve a quadratic using the polynomial solver tool in Equation mode or with SolveN, found in the Catalog menu.

But you can also go a step further and graph the function in Graph and Table mode, demonstrating how the same solutions appear as x-intercepts on a curve.

Modelling these approaches side by side highlights not only that the calculator can confirm answers, but that it can also reveal the connections between algebraic and graphical representations.

This could help to move students away from a rigid, ‘right way’ mindset and towards an understanding that, in maths, everything is connected, meaning different methods can complement each other.

Building confidence through immediate feedback

Another key benefit of modelling calculator use is the instant feedback it provides. When you demonstrate a calculation step by step, students see the result instantly and can question whether it makes sense.

This encourages mathematical thinking, but just as importantly, it shows that mistakes are part of the learning process. Getting something wrong, questioning it and correcting it in front of the class shows the value of resilience and also highlights the importance of checking work carefully.

In a trigonometry lesson, for instance, you could be looking at a right-angled triangle problem like finding the height of a tree given the angle of elevation and the distance of an observer from the base.

Students may already know that this should be approached as a tan calculation, since the unknown side is opposite the angle and the known side is the adjacent. You could then test their knowledge and how much attention they’re paying by deliberately entering a cos calculation on a ClassWiz scientific calculator.

This would give an answer that may look plausible but is incorrect, prompting discussions about why it’s wrong in the context of trigonometric theory.

You could also use this as an opportunity to emphasise what calculators can and can’t do. The handset provides answers based on inputs, but it’s down to the student to interrogate whether those answers make sense in the context of the question. If not, they can investigate where they might have made a mistake earlier in their working.

Moving beyond rote learning to real understanding

By demonstrating calculator use in your lessons, you can help students see maths as more than a set of formulas to memorise. They start to recognise patterns, explore relationships and develop a deeper grasp of why methods work.

Showing how calculators can test, verify and visualise results also encourages students to move beyond routine recall and repetition, towards genuine understanding and mathematical thinking.

You might, for example, be teaching a class about exponential growth. Using the Table function on a ClassWiz calculator, you can input f(x) = 2^x and display outputs for different values of x.

Students will immediately see how quickly the results escalate as x increases, to the point that, when x = 20, the corresponding value in the f(x) column is already in the millions.

This can spark discussions about concepts such as population growth or compound interest, shifting the focus from simply calculating a power to the behaviour of a function and why it matters.

Tools and resources to support your teaching

Effective modelling of calculator use is partly about having the right tools to offer clear demonstrations and the resources to support structured, successful lessons.

ClassPad, Casio’s web-based virtual learning environment, includes emulators for both scientific and graphic calculators. These allow you to project your calculator screen directly to the class, making it easy to demonstrate methods in real time.

Students can follow each step, see exactly which keys you’re pressing and compare the emulator’s display with their own. This helps keep the whole class engaged and ensures that no-one is left behind.

You can also access an extensive library of teaching resources on the Casio Education website, including downloadable activities, worksheets and worked examples designed to help you integrate calculators into lessons effectively.

Tools like ClassPad and focused resources can offer valuable support as you show students multiple approaches, reinforce key concepts and encourage independent exploration.