How graphing technology deepens student understanding of quadratic graphs and equations

As students explore quadratic graphs and equations, the visualisations available when using graphing technology can help them grasp the concepts more easily and deepen their understanding. We spoke with mathematician Simon May to find out how using a graphing calculator in the classroom enhances the learning experience compared to using scientific calculators.

Comparing scientific and graphic calculators

When comparing the two devices, the main difference is that one can draw graphs of functions, and the other can’t. Students can easily enter a quadratic on the ClassWiz, and find particular values using the CALC function . That allows them to say what happens when x has a specific value. For instance, for the quadratic function, entering x= 3, the ClassWiz calculator will tell students the quadratic has a particular value of 2, asking, “What is the value of the function f(x)?” This example is one of the starting points students may look at when dealing with a function saying, “What values has it got? What relationship is there between a y value and the x value?” 

There is also a Table function on the calculator that does allow students to enter a function again. However, students must enter the function again; it’s not automatically carried over from anywhere. Students can then set a table range, going up in integer values perhaps; they can scroll down and see it does confirm that when x =3, y has a value of 2. 

If you compare that to the graphing calculator, it also has a Table function, and it’s almost the same input; students can limit the range of values and get the same table. There isn’t a direct f(x) function on the graphic calculator, but variable values can be used with the History function. However, this is handled more effectively in Graph mode. One of the nice things about graphing calculators is that after students enter the value in Table or Graph, it’s automatically carried over to Table or Graph and doesn’t need to be re-entered. 

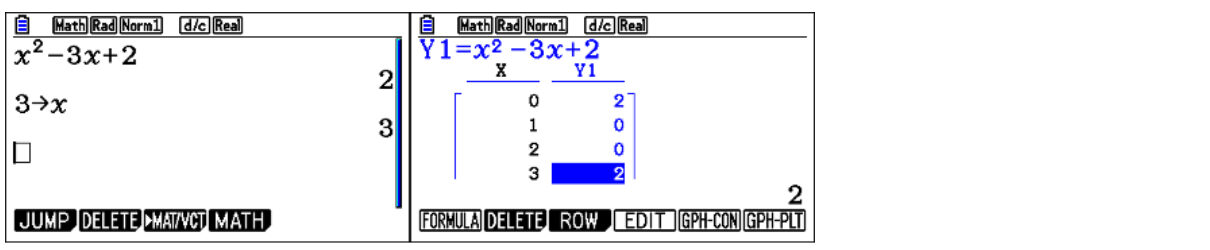
Visualisations encourages discussion and further investigation

Once students have a table of values, they can graph continuously or plot a point. It gives students a rough idea of the shape, which is nice because when they get onto harder functions later, like cubics and quartics, they will be asked to sketch such things. This visualisation promotes a discussion around the shape. Could it be U-shaped? Could it be a quartic, in which case it would be W-shaped? Does it go below the x-axis? Is it smooth between two and three? 

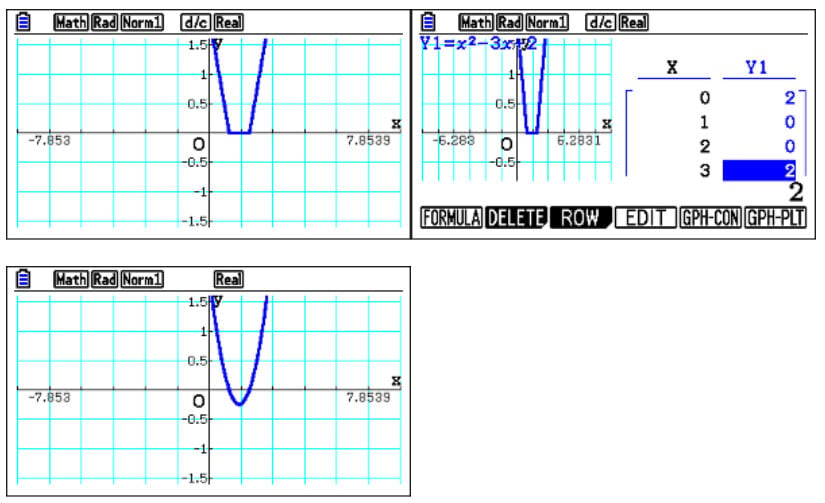
You can take the discussion further, asking, “What happens if we graph it continuously?” which joins up the two calculated points. So then, again, this also promotes discussion about, “Do you think this is a straight line version of the curve? Could it be something else?” But when students go to graph mode, one of the main benefits is they can draw it, confirming that it is a smooth curve below the x-axis. Students then have a much better idea of how it will look.

The scientific calculator allows students to say, “What do these zeros mean in Table mode?” When x is one, y is zero; when x is two, y is zero, which are the roots. When students have zeros in that column, they can factorise it. On the graphing calculator, students can directly enter the factorised version, and can surmise what the factorised version is and can then sketch it. And because both graphs drawn are coincidental, it confirms that the factorisation is correct. 

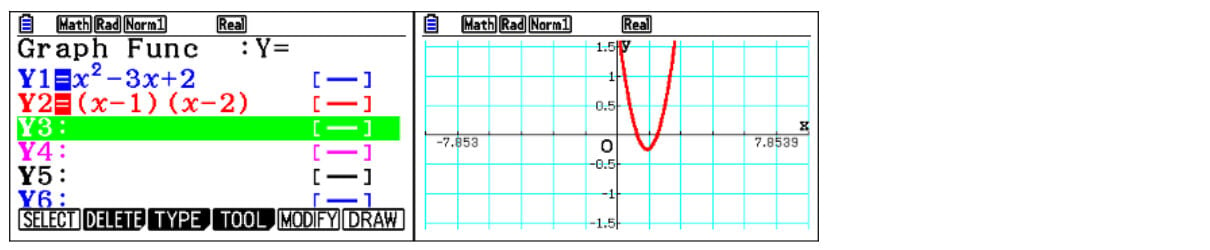
Students can attempt to do it on the ClassWiz, by entering the factorised version to compare the two functions. But it’s not graphical, and it’s not as clear that they are the same function. If students keep pressing zero on the scientific, it gives them the vertex value, which is the lowest point in this case. The graphing calculator can provide a decimal value, but it will automatically display as a surd.

Using the graphing calculator functionalty to deepen exploration

One of the most useful differences with the graphing calculator is SolveN, which can solve a quadratic, even in factorised form. Students don’t have to set it to zero because it assumes it’s set to zero. And it provides both solutions exactly. 

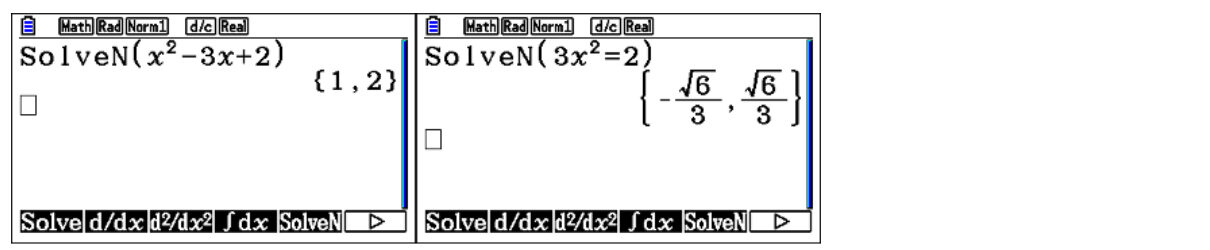
The limitation of the scientific calculator is that students can only use Solve to find a single decimal root at a time, and students need to start at an appropriate beginning point.. It’s a more convoluted and less efficient way of solving quadratic. 

On the scientific, students can find a table of values and attempt to find a range for its roots. If they use equation solving, they can also find the vertex of a quadratic. 

Depending on what you’re trying to teach, you might be interested in the gradient or how steep the quadratic is. When discussing calculus and differentiation, students can go to table mode and enter their function. But then students can also differentiate the function, which provides a table of values. Students have x and y values and the gradient function, which they can investigate numerically. However, they are only limited to these two functions.

The graphic calculator has a derivative function that students can turn on. When students enter Table mode, they don’t have to enter the derivative as a function because the calculator will automatically create a column of values for both y and the gradient values, And they are not limited to just a single function and it’s derivative.

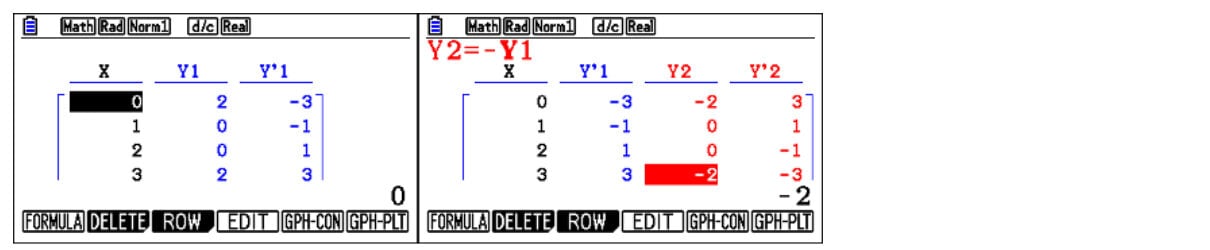
When students go to Graph mode, they can also draw, which is the advantage of the graphing calculator and enables easy analysis of the function. For instance, the Trace function allows them to move a point along the function, and at every point, it will display both the x and y values. With the derivative on, it also shows the derivative value. Students can easily enter a particular value if they’re interested in that, akin to creating a table of values.