Understanding vectors in A-level maths: theory, applications and real-world uses
We explore the topic of vectors in A-level maths, look at real-world applications of this concept and recommend some useful resources.

As you make your way through the various challenges of A-level maths, vectors is one of the key topics you’ll need to get to grips with.
In this article, we hope to demystify this aspect of the syllabus a little by providing:
• A quick definition of vectors to refresh your memory
• A recap of how this topic is covered in pure maths and mechanics
• Some examples of how vectors are used in the real world (i.e. how the theory is put into practice)
• Some tips and resources to help you better understand vectors ahead of A-level maths exams
What are vectors?
In the context of A-level maths, vectors are quantities that have both magnitude (size) and direction. This distinguishes vectors from scalars, which only have magnitude. Vectors are commonly used to represent movement, force and direction in both pure maths and mechanics.
They can be represented as:
• Arrows (showing direction and length)
• Coordinate pairs or triplets
• Letters in bold, or with an arrow above – for example: ![]()
Basic vector operations include:
Addition/subtraction: Combine or reverse direction
Scalar multiplication: Stretch or shrink a vector’s length without changing direction

How are vectors covered in A-level maths?
Vectors appear in various areas of the A-level maths syllabus, with content split between pure maths and mechanics. In pure maths, you’ll learn vector notation, magnitude and direction, and how to solve geometric problems using vector equations of lines. You’ll also work with the dot product and vector proofs.
In mechanics, vectors are used to describe motion, forces and acceleration. You’ll apply vector techniques to solve real-world problems involving direction and magnitude.
Exam boards like Edexcel, AQA and OCR all include vectors in their A-level papers, though specific topics and question styles may vary slightly between them.

Working with vectors: exam-style examples
Once you understand the basics of vectors in A-level maths, practising exam-style questions is a good way to build confidence. Here are two examples, along with some tips on how a Casio graphic calculator can help you out.
Example 1: Find the magnitude and direction of a vector
Let a = (3, 4). Find its magnitude and the angle it makes with the x axis.
Magnitude:
Use the formula |a| = √(x² + y²)
|a| = √(3² + 4²) = √(9 + 16) = √25 = 5
Direction 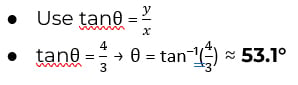
You can use your graphic calculator’s vector magnitude, square root and inverse tan functionality to speed up all or part of these processes and check your answers.
Example 2: Show that a point lies on a line
Line:r = (2, 1) + λ(1, 2). Is point P(5, 7) on the line?
Check:
(5, 7) = (2, 1) + λ(1, 2)
Solve:
λ = 3 works for both x and y, so P lies on the line
On a Casio graphing handset, try plotting both the point and line visually to confirm your answer.
Vectors in the real world: applications and examples
Vectors aren’t just a theoretical concept that only comes up in maths lessons and exams. In fact, they have a wide range of practical uses in the real world.
From calculating movement and direction to modelling forces and designing graphics, vectors help solve problems in engineering, science and everyday technology.

Navigation and GPS
Vectors play a key role in vital processes such as guiding aircraft, ships and even smartphones. They’re essential for determining direction, displacement and changes in position.
Specific applications include:
• Calculating the direction and distance between locations
• Determining a vehicle’s heading relative to wind or current
• In GPS technology, calculating changes in position using displacement vectors
• Modelling aircraft positions in air traffic control systems, thereby avoiding collisions
• Guiding sat-nav users from one point to another efficiently

Physics and engineering
In physics and engineering – two areas you may well be looking at for a future career if you’re studying A-level maths – vectors describe quantities that have both size and direction. This makes them essential for accurate modelling and calculations.
They’re commonly used to:
• Represent forces acting on a structure (tension, gravity and friction, for example)
• Model acceleration, velocity and momentum in motion equations
• Analyse balanced and unbalanced forces in equilibrium problems
• Describe currents and fields in electrical engineering
• Calculate the result of multiple vector forces acting on an object

Computer graphics and animation
In the field of digital design, vectors can help to bring 2D and 3D graphics to life in the most precise and realistic way.
• They can be applied to processes such as:
• Defining the positions and movements of objects in animations
• Scaling, rotating and transforming shapes in design software
• Describing lighting directions and reflections for realistic rendering
• Allowing smooth interpolation between frames in animation
• 3D modelling to define surface normals and object orientation

Robotics
Another highly innovative and fast-moving field, robotics relies on vectors to control movement, orientation and interaction between an object and its environment.
Vectors make it possible for professionals in this industry to:
• Calculate joint movements and angles for robotic arms
• Formulate pathfinding algorithms to plan movement through space
• Represent direction and speed in autonomous vehicle systems
• Model sensor data for obstacle detection and avoidance
• Describe torque and force vectors in mechanical design

Other applications
Vectors crop up in many areas outside of science and engineering, and can have all sorts of influences on daily life. For example:
Sports: Analysing player movement and ball trajectories
Meteorology: Describing wind speed and direction
Economics: Representing multi-variable trends or quantities
Architecture: Modelling structural forces and stress points

Understanding vectors: resources and calculator tips
A Casio graphic calculator is a powerful tool that can give you a lot of help and support as you learn vectors for exams.
The recently launched fx-CG100 can perform vector operations including addition, subtraction and scalar multiplication. You can also visualise results for better understanding.
Furthermore, you can use your calculator for tasks such as:
Entering and manipulating vectors using coordinate form
Calculating magnitudes and dot products
Solving problems involving vector equations and linear combinations
We also recommend taking full advantage of the many free resources available that cover vectors, including Bicen Maths’ videos summarising vectors in two dimensions and vectors in three dimensions.
Blog
- Graphing technology
- Scientific calculators
- Exams
- Curriculum
- Classroom
- Students




















