Understanding the modulus function: a comprehensive guide
What do students need to know about the modulus function to ensure they can approach these questions with confidence in exams?
The modulus function is a very popular topic for questions in A-level maths exams, so it’s important that students are comfortable with what this involves and have an understanding of what they may be asked to do in a paper.
While it’s vital they know how to deal with modulus functions algebraically, a calculator is a great way to help students understand the topic, as they can actually draw it and approach it graphically.
So what do your students need to know about this topic in order to stand the best chance of success in exams?

What is a modulus function?
The modulus refers to the magnitude of a number, regardless of its sign. It is denoted by two straight lines either side of a function or variable – |x| – which represents the non-negative value of x.
A simple way to think of it is as representing the distance from 0 on the number line. As a result, it’s sometimes referred to as the absolute value of a number.
The modulus function is used to calculate the absolute value or magnitude of a number, and will give the same answer irrespective of whether the number is positive or negative.

Key properties of modulus functions
When dealing with the modulus function, there are several formula variations to be aware of, as the value of the modulus will always be positive. These formulae appear as follows:
If x is positive, then f(x) = x
If x = 0, then f(x) = 0
If x is negative, then f(x) = -x
For example, for the modulus function f(x) = |x|, then:
If x = −5, then y = f(x) = f(−5) = −(−5) = 5
If x = 5, then y = f(x) = f(5) = 5
If x = 0, then y = f(x) = f(0) = 0
The modulus function always gives a non-negative number as output for all real values of x. Therefore, the modulus function is never equal to a negative number.
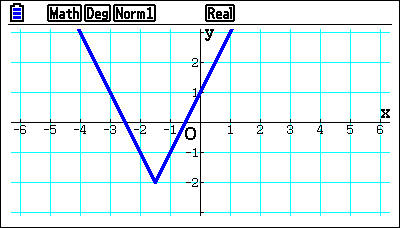
What do modulus function graphs look like?
When answering exam questions, students will need to understand the relationships between the functions they’ve been given. It’s easy for students to get lost in the algebra and lose sight of this when solving numerically, leading to incorrect answers. For this reason, it’s often a good idea to visualise the solutions with the help of a graph. This lets students see at a glance how many intersection points there are.
When graphed, modulus functions often have a characteristic V shape. For linear functions this will consist of two straight lines that join at a vertex.. Technically, this means that graphing modulus functions can be considered a transformation of part of the domain a function.
This can provide a simple way to identify a modulus function. Indeed, specifications for syllabuses even state that it will be a V-shaped graph. However, there have been questions in exams where students are asked to perform transformations of graphs that are not straight lines, such as a sine curve.
Step-by-step guide to graphing modulus functions
When plotting a modulus function graph by hand, students should start by creating a table for the values of x and y they can then plot onto a graph. However, using a graphic calculator can make these operations faster, easier and more accurate.
The Casio fx-CG50, for example, has inbuilt tools that assist with modulus functions, which can be used in any exam where calculator use is allowed.
To plot a modulus function graph on the fx-CG50, the following steps are required.
Select Graph from the main menu
To enter a modulus function, press OPTN and choose Numeric (F5)
Select the Abs key (F1)
Enter the function in the Y1 field, then press EXE
To plot the function, choose DRAW (F6)
The function can then be analysed as usual with G-Solve.
We’ve created the following video to illustrate this process, which also shows how modulus functions can be solved numerically using the G-Solv feature.
However, this doesn’t mean students using scientific calculators are left out. While these devices can’t be used to directly graph functions, the new ClassWiz fx-991CW does have new functionality that allows students to solve equations or evaluate functions that can be used when dealing with modulus functions. So, for example, students are able to save a function as f (x) and then evaluate this as f for a particular value, or evaluate the absolute value of a function.

Applications of modulus functions in real life
Demonstrating to students how the modulus function can be applied to real-world scenarios is always a good way to engage them with the materials and look beyond what they can expect in the exam.
For example, one common situation that relies on the modulus function is GPS navigation. If you’ve used this, you’ll have noticed that the distance shown between your location and the destination is always a positive number – and this remains the case even if you drive past it. This is because the modulus function is being used in the GPS’ calculations.
In finance, the modulus function is useful in evaluating things like changes in the value of a stock price. Because these can be up or down, being able to understand the absolute value of these changes as a positive number helps show the magnitude of any shifts. This makes it easier to see patterns and predict what may happen in the future.
Adding such real-world examples to lessons could help students understand what they can do with the modulus function and provides context to these questions, building an understanding of how the function works and where it can be applied.
Blog
- Graphing technology
- Scientific calculators
- Exams
- Curriculum
- Classroom
- Students


















